コンデンサ(キャパシタ)

コンデンサガイド
C=ε×S/dの公式によると、コンデンサの静電容量を大きくする方法としては
次の3種類があります。
① ε(誘電率)を大きくする
② S(電極面積)を大きくする
③ d(誘電体厚み)を小さくする
ここで①②については直感的にイメージしやすいのですが、③については逆に誘電体が厚い方がたくさんの電荷が溜められそうな気もしますが、そうではありません。
これは電荷は2つの電極に溜まるものであり、誘電体の中に溜まるものではないからです。
まずはこの点をご理解いただいた上で、式がどのように導かれたのかを説明します。これからは無味乾燥な数式が並んでしまいますが、どうかご容赦ください。
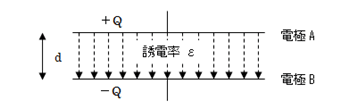
図1に示す電極にはさまれた空間に電圧を印加した時にできる電界の大きさE[V/m]は、電圧をV[V]、電極間距離をd[m]とすると(1)式となります。
E=V/d [V/m] ・・・(1)
この電界は電源から入り込んだ電荷でつくられますが、これを電気力線で考えると、ガウスの定理から+Q[C]の電荷からはQ/ε[本]の電気力線が出るので、図1において電極AからはQ/ε[本]の電気力線が出て電極Bに入ります。
電気力線はその密度が電界の大きさに等しくなるので、電極の面積をS[m2]とすれば(2)式の関係が成り立ちます。
V/d=(Q/ε)/S ・・・(2)
これを電源から入り込んだ電荷Qについて整理すると(3)式になります。
Q=ε×SV/d [C] ・・・(3)
(3)式から分かるように、電荷Qは印加電圧に比例するので、コンデンサの性能は単位印加電圧あたりに溜められる電荷量で表すのが良く、静電容量をC[F]とすると次式のようになります。
C =Q/V [C/V=F] ・・・(4)
この式から、静電容量Cは電荷Qに比例することが分かるので、静電容量を大きくするには、図1の電極AとBに溜まる電荷Qを大きくすれば良いと言うことになります。
では、電荷Qを大きくするにはどうしたら良いでしょう?
(3)式を見ると、電荷Qは電極間距離dに反比例することが分かります。
つまり、電極間距離が小さくなればなるほど、電荷Qは大きくなります。
以上のことを簡単にまとめると、電極間距離dが小さくなればなるほど、電極AとBに溜まる電荷Qは大きくなり、溜まる電荷Qが大きくなるので静電容量Cも大きくなる。このように理解すれば、少しは直感的に分かるのではないかと思います。
(3)式と(4)式より、おなじみの(5)式が導かれます。電極間距離dが小さいほど、静電容量Cが大きくなることを数式で導くとこのようになります。
C=ε×S/d [F] ・・・(5)
株式会社 福井村田製作所 第1コンデンサ商品開発部 N.S
記事の内容は、記事公開日時点の情報です。最新の情報と異なる場合がありますのでご了承ください。