Capacitor

Capacitor Guide
According to the formula C = ε × S/d, there are three different methods for increasing the electrostatic capacitance of a capacitor, as follows:
①Increase ε (dielectric constant)
②Increase S (electrode area)
③Reduce d (thickness of dielectric)
Here, ① and ② are intuitively easy to imagine, but regarding ③ it would appear that a thicker dielectric would instead be able to accumulate a greater charge.
That is not the case, however, as the charge accumulates at the two electrodes instead of inside the dielectric.
First, I will explain this point, and then describe how the formula was derived. Please bear with the many cut-and-dried numerical formulas that follow.
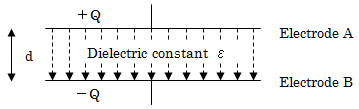
Labeling the voltage as V [V] and the distance between electrodes as d [m], the size of the electric field E [V/m] generated when voltage is applied to the space between the electrodes shown in Fig. 1 is given by Eq. (1).
E = V/d [V/m] ・・・(1)
This electric field is generated by the charge that flowed in from the power supply. However, thinking in terms of electrical force lines, and according to Gauss's law, Q/ε [lines] number of electrical force lines extend from the +Q [C] charge. Therefore, in Fig. 1, Q/ε [lines] number of electrical force lines extend from electrode A to electrode B.
The density of these electrical force lines is equal to the size of the electric field, so labeling the electrode area as S [m2], the relationship shown in Eq. (2) is established.
V/d = (Q/ε)/S ・・・(2)
Arranging this according to the charge Q that flowed in from the power supply results in Eq. (3).
Q = ε × SV/d [C] ・・・(3)
Eq. (3) shows that the charge Q is proportional to the applied voltage, so capacitor performance can be expressed in terms of the charge level that can be accumulated per unit applied voltage, and labeling the electrostatic capacitance as C[F] yields the following equation.
C = Q/V [C/V = F] ・・・(4)
This equation shows that the electrostatic capacitance C is proportional to the charge Q, so in order to increase the electrostatic capacitance, the charge Q that accumulates at the electrodes A and B in Fig. 1 should be increased.
Then, how can the charge Q be increased?
Eq. (3) shows that the charge Q is inversely proportional to the distance between electrodes d.
That is to say, the charge Q increases as the distance between electrodes decreases.
To briefly summarize the above, the charge Q that accumulates at the electrodes A and B increases as the distance between electrodes d decreases, and the accumulating charge Q becomes larger so the electrostatic capacitance C also increases. I think that understanding the phenomenon in this manner makes it a little more intuitive.
The familiar Eq. (5) is derived from Eq. (3) and Eq. (4). This is how the principle that the electrostatic capacitance C increases as the distance between electrodes d decreases is derived using numerical formulas.
C = ε × S/d [F] ・・・(5)
N.S., MLCC Product Development Dept. 1, Fukui Murata Manufacturing Co., Ltd.
The information presented in this article was current as of the date of publication. Please note that it may differ from the latest information.